비교 상품 소개

QQQ 상품의 일일 수익률을 5배로 추종하는 QQQ5.L 상품의 최근 1년 성과를 살펴봅니다.

주의: 해외 종목은 야후 파이낸스 데이터를 이용합니다. 야후 파이낸스는 종목에 따라 배당 내역 일부가 누락되어 있을 수 있습니다. 이로 인해, 배당 재투자를 가정하여 비교한 분석 결과는 부정확할 수 있습니다. 참고: 야후 파이낸스 수정 > 주가 오류 (일부 분배/배당 내역 누락으로 인한 부정확한 TR값)

주의: 해외 종목의 주가는 야후 파이낸스 데이터를 이용합니다. 종목이 액면 분할/병합될 경우 배당금이 보정되지 않으면, 배당 재투자 가격(TR; Total Return)이 과대/과소 추정될 수 있습니다. 최근 1 : 3으로 액면 분할한 SCHD의 경우에도, 실제보다 높은 배당 재투자 수익률로 표기되고 있습니다. 다른 사이트를 이용하여 다시 한 번 확인하길 권합니다. 사이트 예: ETF CHECK

주의: 개별 종목의 상장 기간은 다를 수 있습니다. 상장 기간이 짧은 종목을 기준으로 정렬합니다.

주의: 야후 파이낸스의 레버리지/인버스 종목의 가격은 부정확할 수 있습니다. 상장 중 레버리지/인버스 배율이 변경된 경우에는 이를 제대로 반영하지 못할 수 있습니다.

주의: 개별 종목의 상장 기간은 다를 수 있습니다. 최대 최근 1년간 성과 데이터를 바탕으로 계산/추정하였기에, 상장 기간이 다른 상품과 직접적으로 비교할 수 없습니다. 개별 레버리지/인버스 페이지의 세부 내용을 확인할 필요가 있습니다.

종목 CAGR 편차 샤프 MDD AvDD
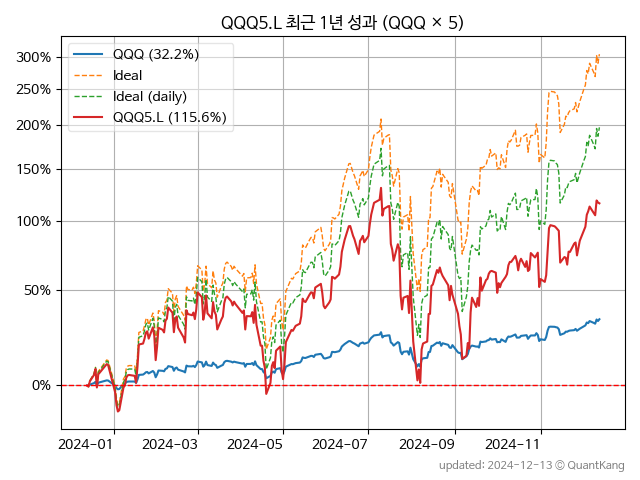
QQQ5.L 115.6% 85.9% 1.34 -56.1% -16.8%

QQQ5.L

주요 가격 변동 지표1

종목 CAGR 편차 샤프 MDD AvDD
QQQ 32.2% 17.5% 1.84 -13.6% -2.4%
Ideal2 304.2% 87.4% 3.48 -51.7% -10.8%
I. daily3 196.9% 87.6% 2.25 -55.0% -14.0%
QQQ5.L 115.6% 85.9% 1.34 -56.1% -16.8%

추정 비용4

QQQ5.L 상품을 QQQ 상품의 5배 레버리지라 가정하고 분석한 결과입니다.

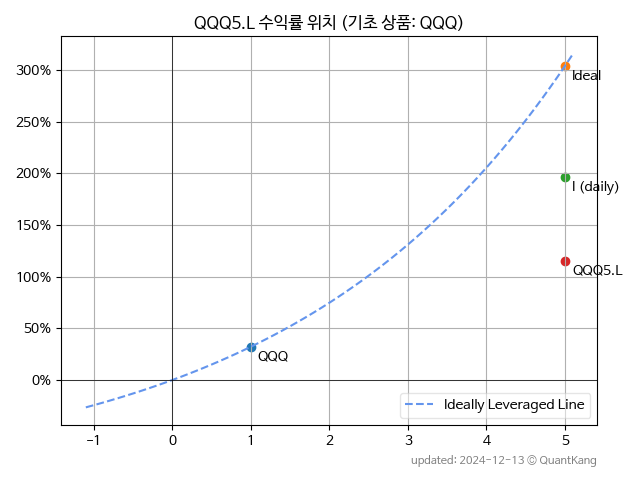
QQQ5.L

종목 변동성비용5 금융비용6 전체비용7
QQQ5.L 26.6% 27.5% 46.7%

관련 레버리지/인버스 상품의 수익률 분포

QQQ 상품을 기초로 하는 타 레버리지/인버스 상품과 비교합니다. 상장된지 1년 미만인 상품은 다른 상품과 직접적으로 비교할 수 없습니다.

QQQ

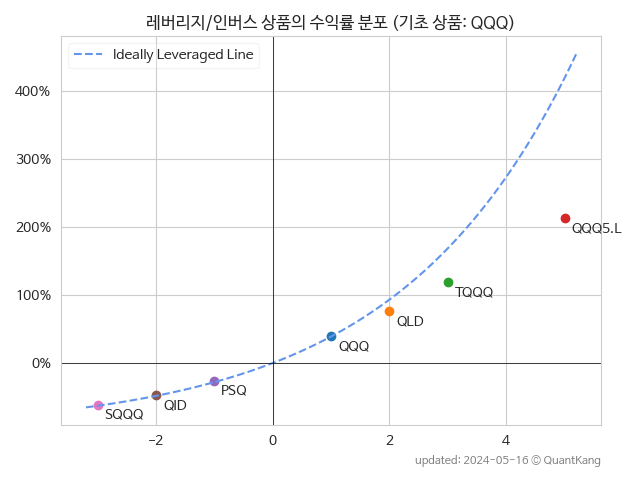
종목 배율 CAGR 변동성비용 금융비용 전체비용
QQQ   32.2% - - -
QLD 2x 58.6% 3.0% 6.5% 9.3%
TQQQ 3x 86.0% 8.8% 11.8% 19.6%
QQQ5.L 5x 115.6% 26.6% 27.5% 46.7%
PSQ -1x -19.6% 3.0% -9.6% -6.3%
QID -2x -40.1% 8.8% -14.9% -4.8%
SQQQ -3x -57.1% 16.8% -19.2% 0.9%

관련 정보

  1. 모든 지표는 최근 1년 데이터만을 이용하며 산출합니다. 거래된지 1년 미만인 종목은 해당 기간을 연단위로 환산해서 추정합니다. 편차는 표준편차를 말합니다. 표준편차는 일일 변동성으로 추정한 연단위 변동성입니다. 샤프(Sharpe)는 1년 수익률 / 연단위 표준편차입니다. MDD(Maximum Drawdown) 최대 낙폭(손실폭)입니다. DD(Drawdown)은 현재 낙폭입니다. AvDD(Average Drawdown)은 평균 낙폭입니다. MARr(Managed Account Reports Ratio)은 1년 수익률 / MDD입니다. Calmar Ratio라 불리기도 합니다. ↩

  2. 연속적으로 변하는 수익률을 레버리지 배율만큼 지속적으로 추종하면서, 금융 비용도 발생하지 않는다고 가정한 경우입니다. 연속성을 가정했기에 변동성 비용도 발생하지 않습니다. ↩

  3. 비연속적인 기초 상품의 일단위 수익률을 레버리지 배율만큼 추종하면서, 금융 비용이 없다고 가정한 경우입니다. 비연속성을 가정했기에 변동성 비용은 발생합니다. ↩

  4. 레버리지 상품의 주된 비용인 1. 변동성 끌림(Volatility Drag)에 의한 변동성 비용과 2. 스왑(Swap) 등 차입에 소요되는 금융 비용으로 나누어서 분석합니다. 단순히 두 가지 비용만 가정하고 일일 주가 변화 데이터를 이용하여 추정한 값이므로 실제와 상당한 오차가 있을 수 있습니다. ↩

  5. 연속적이지 않은 기초 상품의 일단위 수익률을 레버리지 배율만큼 추종하는 과정에서 변동성 끌림이 발생합니다. 변동성 비용은 이 변동성 끌림에 의한 발생하는 비용입니다. ↩

  6. 금융 비용은 레버리지 배율을 맞추기 위해 타기관에 스왑(Swap) 등의 형태로 기초 자산을 차입하는데 필요한 비용입니다. 투자자 자금만큼 은행에서 대출 받아 2배 레버리지 투자를 한다면, 은행에서 빌린 자금에 대한 대출이자가 나가게 되는 것과 동일한 원리입니다. 스왑 방식의 경우 대략 (레버리지 배율 - 1) × 해당 지수 또는 종목 차입을 위한 이자율 비용이 발생합니다. 인버스 또는 인버스 레버리지 상품의 경우 대부분의 투자금을 현금으로 보유하고 선물 등 유지 비용이 적게 드는 방식으로 상품을 구성할 수 있습니다. 이 경우 금융 비용이 거의 나가지 않거나 경우에 따라서는 보유 현금(주로 채권에 투자)이나 선물 롤오버 과정에서 수익이 발생할 수 있습니다. 이 경우 금융 비용은 마이너스 값이 나올 수 있습니다. 또한 대상 상품의 총보수에 의해서도 비용 추정에 있어 상당한 오차가 발생할 수 있습니다. 전반적으로 인버스 또는 인버스 레버리지 상품에 대한 추정 금융 비용은 신뢰하기 어려우니 단순 참고용으로 활용하기 바랍니다. ↩

  7. 변동성 비용과 금융 비용을 합한 것입니다. 이 비용은 산술합으로 계산되지 않습니다. 예를 들어 변동성 비용이 10%, 금융 비용이 10%라면 전체 비용은 20%가 아닌 1 - (1 - 10%) × (1 - 10%) = 19%로 계산됩니다. ↩

업데이트: