비교 상품 소개

TIGER 미국배당다우존스타겟커버드콜2호 (458760) 상품과 KODEX 미국S&P500TR (379800) 상품의 성과를 수익률과 위험도로 비교합니다.

주의: 해외 종목은 야후 파이낸스 데이터를 이용합니다. 야후 파이낸스는 종목에 따라 배당 내역 일부가 누락되어 있을 수 있습니다. 이로 인해, 배당 재투자를 가정하여 비교한 분석 결과는 부정확할 수 있습니다. 참고: 야후 파이낸스 수정 > 주가 오류 (일부 분배/배당 내역 누락으로 인한 부정확한 TR값)

주의: 해외 종목의 주가는 야후 파이낸스 데이터를 이용합니다. 종목이 액면 분할/병합될 경우 배당금이 보정되지 않으면, 배당 재투자 가격(TR; Total Return)이 과대/과소 추정될 수 있습니다. 최근 1 : 3으로 액면 분할한 SCHD의 경우에도, 실제보다 높은 배당 재투자 수익률로 표기되고 있습니다. 다른 사이트를 이용하여 다시 한 번 확인하길 권합니다. 사이트 예: ETF CHECK

주의: 개별 종목의 상장 기간은 다를 수 있습니다. 상장 기간이 짧은 종목을 기준으로 정렬합니다.

지난 성과

두 상품의 성과를 비교할 수 있는 가장 긴 기간은 최근 1년 5개월입니다. 아래는 이 기간의 성과1를 그래프와 표로 나타낸 것입니다. 그래프 범례에서 괄호안의 퍼센트 수치는 CAGR2입니다. 하단의 보조 그래프는 KODEX 미국S&P500TR 대비 TIGER 미국배당다우존스타겟커버드콜2호의 비를 나타냅니다. TIGER 미국배당다우존스타겟커버드콜2호의 수익률이 KODEX 미국S&P500TR보다 지속적으로 우세하면 상승하고, 반대의 경우에는 하락합니다.

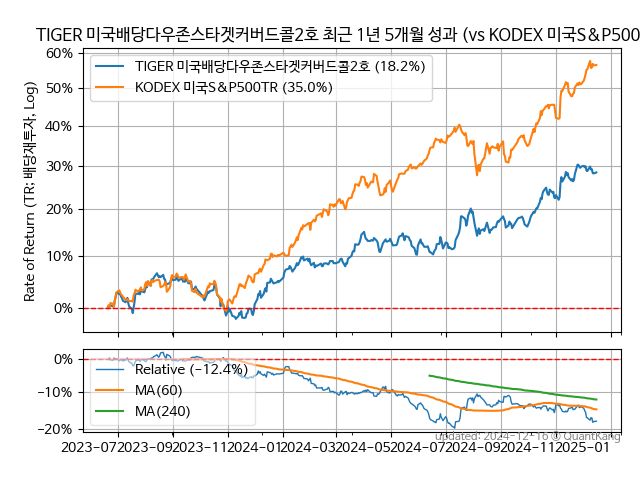
TIGER 미국배당다우존스타겟커버드콜2호

종목 CAGR 편차 샤프 MDD AvDD
TIGER 미국배당다우존스타겟커버드콜2호 18.2% 10.7% 1.71 -8.1% -2.0%
KODEX 미국S&P500TR 35.0% 12.0% 2.92 -8.9% -1.4%

성과를 분석하는 전통적인 방법인 수익률과 위험도3를 살펴봅니다.

수익률 지표 (CAGR): TIGER 미국배당다우존스타겟커버드콜2호의 CAGR은 18.2%로 KODEX 미국S&P500TR의 35.0%보다 -16.8% 낮았습니다. (낮은 수익률)4

위험도 지표 (표준편차): TIGER 미국배당다우존스타겟커버드콜2호의 표준편차는 10.7%로 KODEX 미국S&P500TR의 12.0%보다 -1.3% 낮았습니다. (낮은 위험도)

위험도 지표 (MDD): TIGER 미국배당다우존스타겟커버드콜2호의 8.1%의 MDD는 KODEX 미국S&P500TR의 8.9%와 비슷했습니다. (비슷한 위험도)

동일 수준 위험 노출을 위한 비중 조절

수익률과 위험도가 다른 상품을 비교하는 방법의 하나는, 둘 중 하나를 동일하게 설정하고, 나머지 하나를 비교하는 것입니다. 여기서는 KODEX 미국S&P500TR의 투자 비중5을 조절하여 TIGER 미국배당다우존스타겟커버드콜2호의 위험도와 유사하게 맞추어 수익률를 비교합니다.

위험도 지표 (표준편차): 표준편차를 동일한 값으로 맞추기 위해서는 12.0% / 10.7% = 89% 비중으로 투자하면 됩니다.6

위험도 지표 (MDD): MDD를 동일한 값으로 맞추기 위해서는 8.9% / 8.1% = 91% 비중으로 투자하면 됩니다.

동일 수준 위험하에서의 추정 성과

아래는 비중을 조절한 경우를 추가하여, 그래프와 표에 성과를 기록한 것입니다. KODEX 미국S&P500TRSTD는 표준편차를 맞춘7 경우이고, KODEX 미국S&P500TRMDD는 MDD를 맞춘 경우입니다. 앞에서와 같이 그래프 범례에서 괄호안의 퍼센트 수치는 CAGR입니다.

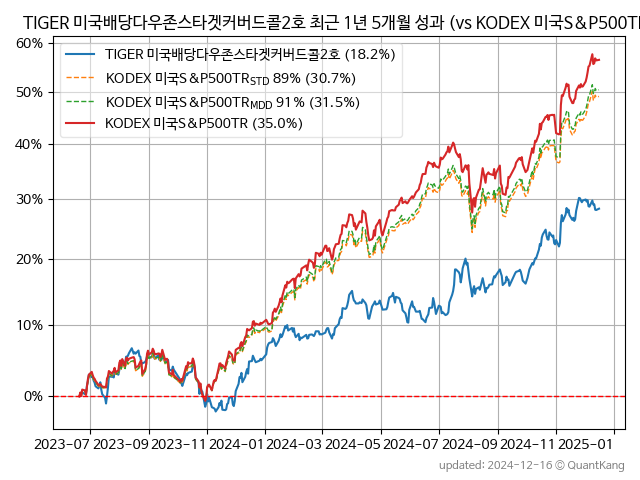
TIGER 미국배당다우존스타겟커버드콜2호

종목 CAGR 편차 샤프 MDD AvDD
TIGER 미국배당다우존스타겟커버드콜2호 18.2% 10.7% 1.71 -8.1% -2.0%
KODEX 미국S&P500TR 35.0% 12.0% 2.92 -8.9% -1.4%
KODEX 미국S&P500TRSTD (89%) 30.7% 10.7% 2.88 -7.9% -1.2%
KODEX 미국S&P500TRMDD (91%) 31.5% 10.9% 2.89 -8.1% -1.3%

각각의 경우를 TIGER 미국배당다우존스타겟커버드콜2호의 성과와 비교해 봅니다.

위험도 지표 (표준편차): 89% 투자 비중으로 표준편차를 비슷한 수준으로 맞추면, CAGR은 30.7%로 TIGER 미국배당다우존스타겟커버드콜2호의 18.2%보다 12.5% 높았습니다. (높은 수익률)

위험도 지표 (MDD): 91% 투자 비중으로 하여 MDD를 비슷한 수준으로 맞추면, CAGR은 31.5%로 TIGER 미국배당다우존스타겟커버드콜2호의 18.2%보다 13.2% 높았습니다. (높은 수익률)

최종 비교

주의 투자 시점과 기간, 그리고 전략에 따라 다른 결과가 나올 수 있습니다. 백테스트 기간이 짧은 경우 통계적 신뢰성이 떨어질 수 있습니다. 미래에도 동일한 경향이 지속된다고 보장할 수 없습니다.

지난 1년 5개월간 거치식으로 투자했다고 가정합니다.

KODEX 미국S&P500TR의 투자 비중을 조절하여 표준편차나 MDD를 동일하게 맞추면, CAGR이 평균 31.1%인 포트폴리오를 만들 수 있습니다. 이 포트폴리오는 TIGER 미국배당다우존스타겟커버드콜2호의 18.2%보다 12.8% 높았습니다.

TIGER 미국배당다우존스타겟커버드콜2호 < KODEX 미국S&P500TR

관련 정보

  1. 가능한 경우 배당까지 고려한 주가 데이터를 이용하였습니다. 현재로는 국내 일반 종목의 경우 배당이 고려되어 있지 않으며, 국내 ETF와 해외 종목은 배당이 고려되었습니다. 각종 수수료, 세금 등 부대비용은 고려되지 않았습니다. ↩

  2. CAGR(Compound Annual Growth Aate, 연평균 성장률)는 해당 기기 동안의 수익률을 연평균 복리 수익률로 환산한 수치입니다. ↩

  3. 리스크(risk)로도 번역되는 위험도는 손실 가능성만을 의미하지 않습니다. 해당 수익률을 달성하는데 얼마만큼의 불확실성이 있는지에 대한 지표입니다. 예를 들어 동일한 연 10% 수익률을 기대하는 상품이라도 최고 수익률이 높은 상품은 위험도가 높다고 판단합니다. ↩

  4. 통계적 분석에 의한 비교가 아닌, 1% 절대값을 기준으로 한 평가입니다. ↩

  5. 투자 비중은 경우에 따라서는 100% 넘을 수 있습니다. 이는 비교 대상보다 더 나은 투자 상품인 경우에 흔히 발생합니다. 투자 비중은 현금을 일부 보유 또는 차입하는 것을 의미합니다. 이 분석에서는 이러한 현금과 관련한 이자 또는 비용은 감안하지 않았습니다. ↩

  6. 표에도 나와 있는 샤프 지수(Sharpe Ratio)를 계산하여 비교하는 방법과 동일합니다. 표에서의 샤프 지수는 무위험 수익률을 0%로 가정하였습니다. ↩

  7. 간단한 수식으로 위험도를 맞추기 위한 비중을 계산했기에, 경우에 따라서는 약간의 차이가 있을 수 있습니다. ↩

업데이트: